尖度

「尖度」（Kurtosis）は統計学における概念で、確率分布の尖り具合、つまりデータの分布が中央にどれだけ集中しているか、または尾部にどれだち極端な値が存在するかを示します。尖度は、分布のピークの鋭さと尾部の太さを測る指標であり、資産運用においては投資ポートフォリオのリスクプロファイルを評価する際に重要な役割を果たします。

尖度の計算

尖度は、データの平均値からの偏差を四乗したものの平均を基に算出されます。数式で表すと、データポイント ��xi​ の平均 �μ からの偏差を四乗し、その平均値を標準偏差 �σ の四乗で割った値です。これにより、データの分布がどの程度尖っているかが数値化されます。

正規分布との比較

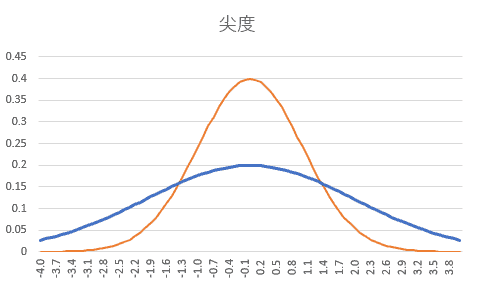
尖度の基準となるのは正規分布で、その尖度は3です。これを超える分布（尖度が3より大きい）は「リーキュルトシス」（leptokurtic）と呼ばれ、より尖ったピークと太い尾を持ち、極端な値が平均値から離れたところに存在しやすいことを意味します。逆に尖度が3未満の分布は「プラティクルトシス」（platykurtic）と呼ばれ、より平坦で尾部が薄いことを示します。

資産運用における尖度の意義

尖度は資産運用において、投資対象のリスク評価に役立ちます。特に、高い尖度を持つ投資対象は、通常のリスクモデルでは予測しづらい極端な価格変動の可能性を秘めているため、これを考慮に入れたリスク管理が必要です。尖度が高い場合、市場の急激な動きや、予期せぬ大きな損失（または利益）が発生するリスクがあります。

ポートフォリオ管理への応用

尖度の分析により、ポートフォリオ内の各資産の分布形状を理解し、それに応じたリスク管理戦略を立てることができます。例えば、高い尖度を持つ資産への投資がリスクを高める可能性があるため、分散投資やヘッジ戦略の適用によりその影響を軽減する措置が考えられます。

尖度は投資のリスクとリターンの関係を深く理解するために不可欠な指標であり、適切な投資戦略を策定する上で非常に有用なツールです。

関連用語： クルトシス